こんにちは！
seiです！
- atcoder始めてみたけど、計算量がわからない
- 問題をみて計算量の見積もりができない
そんなあなたに計算量の見積もり方を説明します！
僕も始めたての頃は計算量がよくわかりませんでした(´;ω;｀)
atcoderを始めて2か月目に突入しました！
※この記事は僕のatcoderスキルが上がるたびに修正を加えていきます。
制限時間とそれに間に合う計算量
atCoderの問題の多くは、実行制限時間が2秒となっています。
大体の目安ですが、2秒以内に計算できる計算量は\(10^8\)以下です。
for文を回して\(10^8\)を超えると危ないです。
オーダー記法について
オーダー記法（O記法）とはアルゴリズムの時間的・空間的な効率性を表現するための記法です。
アルゴリズムの実行時間（またはメモリ使用量）が入力サイズ（n）に対してどのように増加するかを表現する記法です。
オーダー記法のルール
- 定数係数は無視される
- 最も影響力のある項のみが考慮される
例えば以下のコードは入力nを受け取って、\(2n^2+3n+1\)回for文を回しています。
int calculate(int n) {
int result = 0;
for (int i = 0; i < 2 * n * n + 3 * n + 1; i++) {
result++;
}
return result;
}この計算量をオーダー記法で表してみましょう。
まず、定数の係数は無視するので\(n^2+n+1\)
次に影響力のある項のみ残すのでO(\(n^2\))となります。
意味が分かると簡単ですね！
以下はよく見るオーダー達です↓
O(log n)：入力サイズの対数に比例する時間がかかる。一般的に効率の良いアルゴリズムとされる。
O(n)：入力サイズに比例する時間がかかる。
O(\(n^2\))：入力サイズの二乗に比例する時間がかかる。一般的に効率の悪いアルゴリズムとされる。
O(\(2^n\))：入力サイズの指数関数に比例する時間がかかる。非常に効率が悪く、扱いにくいアルゴリズムとされる。
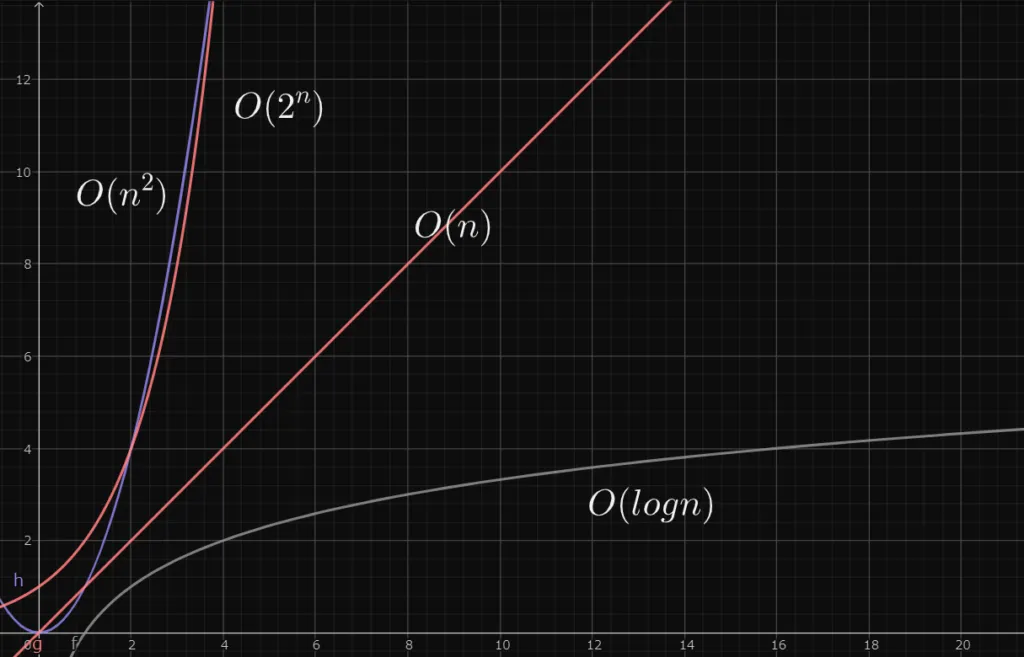
グラフにしてみました！
入力サイズのnが大きくなると、指数が絡む計算量は膨れ上がってしまってるのが分かります。
logの底が気になりますが、二分探索が基本なので、底は2となります！
実際の問題を見積もってみる
atCoderの実際の問題を見積もってみましょう！
以下の問題を考えましょう。
【問題文】
1 以上N 以下の奇数のうち, 正の約数を ちょうど8 個持つようなものの個数を求めよ.
【制約】
N は1 以上200 以下の整数
【解答の方針】
for文を2回使えば解けそうですね。
- 整数nを小さい順に全探索する。
- 全探索している中でさらにその探索中の数字に関して、その数字以下の整数を全探索して割り切れた個数を数える。
nを2回for文で回すので、オーダー記法だと、O(\(n^2)\)で遅そうですが、この問題はそのまま解けます！（全探索）
実際に計算量を見積もってみます。
最悪の場合を想定しないといけないので、n=200で探索中の数字も200と考えると、
\(200×200=40000\) となり\(10^8\)を超えないので、十分間に合いそうです！
【解答のコード】
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, result = 0;
cin >> n;
for (int i = 1; i <= n; i += 2)
{
int yakusuAmount = 0;
for (int j = 1; j <= i; j++)
{
if (i % j == 0)
yakusuAmount++;
}
if (yakusuAmount == 8)
result++;
}
cout << result << endl;
return 0;
}
このように与えられる入力が小さい場合は普通に全探索で解ける場合が多いです。
A,B問題は特に計算量を意識しなくても、そのまま解ける問題が多い気がします。
では、もう一問見積もってみましょう！
果物の値段はそれぞれ\(A_1,A_2,A_3,….A_N\)円である。
- 1≤𝑁≤32
- 1≤K≤min(N,6)
- 1≤Ai≤\(10^8\)
- 入力はすべて整数
【解答の方針】
この問題は果物の選び方を全探索して、合計金額にかかる枚数を数えたらよさそうですが、Nが最大32なので、\(2^{32}\)で\(2^{10}=1024\)ということを考えると\(10^9\)を超えてしまいます。bit全探索（果物を選んでいる状態を0と1の並びで表す)では間に合わなさそうです。
果物を一つずつ選んで合計でK個選んだら終了するDFS(幅優先探索)で解くとよさそうです。こうすれば、果物を選んだ個数がK個に達した瞬間に探索を終わることができるので、選んでいない果物を無駄に探索する必要がなくなります。
ランダウで書くとO(\(2^n\))になりますが、それより少ない計算量で行けるはずです！
【解答のコード】
#include "bits/stdc++.h"
using namespace std;
int n, k, c[10] = {0, 1, 2, 3, 4, 1, 2, 3, 4, 5}, minCoin = 10000000;
long long a[33];
void dfs(long long sum, int takeNum, int nowInd)
{
if (takeNum == k)
{
int tmp_coin = 0;
while (sum > 0)
{
tmp_coin += c[sum % 10];
sum /= 10;
}
minCoin = min(tmp_coin, minCoin);
return;
}
else if (nowInd < n)
{
dfs(sum, takeNum, nowInd + 1);
dfs(sum + a[nowInd], takeNum + 1, nowInd + 1);
}
}
int main()
{
cin >> n >> k;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
dfs(0, 0, 0);
cout << minCoin << endl;
return 0;
}
まとめ
今回はatCoderの計算量の見積もり方について解説しました。
僕も最初の頃は計算量が見積もれなくて訳が分かりませんでした（笑）
特に最初はLeetCodeに取り組んでいたので、計算量の概念が余り身につかなかったのではないかと思っています。
まだまだ早く解くことは難しいので継続していこうと思います！初心者の方は一緒に頑張りましょう！
